그래프 자료구조

그래프란 노드와 노드 사이를 연결하는 간선으로 구성된 자료구조이다. 보통 수학에서 말하는 그래프와는 다른데, 수학의 그것은 차트라고 일컬어진다. 그래프는 아래와 같은 특징을 가진다. 그래프는 어떤 자료들의 관계를 표현하는 가장 일반적인 자료구조라고 할 수 있다.
그래프를 사용하는 예제
수도관 건설
교통망 구성
감염경로
먹이사슬
도로망 건설
그 외 그래프를 사용하는 현실의 예제는 아래의 사이트에 잘 정돈되어있다.
그래프 자료구조의 특징
그래프의 특징은 아래와 같다.
- 그래프는 정점(vertext, 혹은 노드)와 점점을 연결하는 변(Edge)로 구성된다.
- 그래프는 순환구조 혹은 비순환 구조를 가진다.
- 그래프는 방향이 있는 유향 그래프와 방향이 없는 무향 그래프가 있다.
- 그래프는 트리와 다르게 루트의 개념이 없다, 즉 부모 자식이 없다
그래프는 자료구조에서 필수적인 부분이라고 할 수 있다. 왜냐하면 왠만한 자료구조는 이 그래프를 확대 혹은 축소하여 표현할 수 있기 때문이다.
*C++의 stl의 경우 안타깝게도 graph와 tree 자료구조를 제공해주지 않는다. 컴포넌트웨어로는 Boost가 있다.
그래프의 구현
래프를 구현하기 위해서 사용되는 가장 기본적인 두 자료구조는 아래와 같다.
인접 행렬(Adjacency matrix)
인접 리스트(Adjacency list)
인접 리스트를 이용하여 구현한 그래프
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
#include <iostream>
#include <vector>
using namespace std;
struct Edge{
int src, dest, weight;
bool isMarked = false;
};
typedef pair<int, int> Pair;
class Graph{
public:
vector<vector<Pair>> adList;
Graph(vector<Edge> const &edges, int n){
adList.resize(n);
for(auto &edge: edges){
int src = edge.src;
int dest = edge.dest;
int weight = edge.weight;
adList[src].push_back(make_pair(dest, weight));
adList[dest].push_back(make_pair(src, weight));
}
}
};
void printGraph(Graph const &graph, int n){
for(int i = 0; i < n; i++){
for(Pair v: graph.adList[i]){
cout<<"("<<i<<", "<<v.first<<", "<<v.second<<") ";
}
cout<<endl;
}
}
int main(){
vector<Edge> edges = {{0, 1, 1}, {1, 2, 2}, {2, 3, 3}};
Graph graph = Graph(edges, 6);
printGraph(graph, 6);
return 0;
}
|
cs |
노드의 개수가 적을 때는 인접 행렬로 표현하여도 좋지만, 노드의 개수가 많아지면 인접 리스트로 구현하는 편이 비용이 적게 든다. (행렬은 미리 공간을 할당하기 때문에 빈 공간이 많이 생기기 때문이다.)
Depth-First Search(DFS) :깊이 우선 탐색
DFS는 stack이나 재귀호출을 이용하여 구현할 수 있다. 동작은 갈 수 있는 곳까지 한 방향으로 쭉 진행하다가 더 이상 갈 곳이 없다면 이전 상태로 되돌아가는 것이다. 즉, 되돌아 갈 곳을 기억하기 위해 stack이 사용된다.
1. 스택을 이용한 DFS 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
bool visited[7] = { false, };
stack<int> s;
void DFS(Graph const& graph, int start) {
if (visited[start] == false) {
cout<<start<<", ";
s.push(start);
visited[start] = true;
}
while (!s.empty()) {
int now = s.top();
for (auto v : graph.adList[now]) {
if (!visited[v.first]) {//first = dest, second = weight
visited[v.first] = true;
cout<<v.first<<", ";//방문시 출력
s.push(v.first);
break;
}
}
if (s.top() == now) {//조건: for문을 통과했음에도 push된 요소가 없음, 즉 해당 노드가 말단이거나 visit가능한 노드가 존재하지 않음
s.pop();//더 이상 갈 곳이 없으면 pop하여 이전으로 돌아감
}
}
}
|
cs |
1 : 방문 여부를 확인하기 위한 공간이다. 방문시 해당 노드 위치에 true를 할당한다.
9 : 스택이 비는 것이 종료 조건이다.
10 : 스택 상단부터 조사를 시작한다.
11 : 현재 노드(스택 상단 노드)가 갈 수 있는 노드들을 순회하며 갈 수 있으면 스택 상단에 push한다.
16 : 한쪽으로 파고들기 위해 break를 넣어준다. 예를들어 분기가 1->2, 1->3일 경우, 스택에 1을 넣은 상태로, 스택 상단에 2를 넣어 방문처리한다. 이렇게 한 쪽으로 파고들고 끝에 도달하면 다시 1로 돌아온 후, 3으로 가게 될 것이다.
19 : 현재 노드가 더 이상 갈 곳이 없다면 스택을 pop해 기억된 이전 위치로 돌아간다.
위의 과정을 반복한다. 즉, 파고 들어가며 스택을 쌓고, 현재 노드가 더 이상 갈 곳는 끝에 다다르면 스택의 위에서부터 pop한다.
1. 재귀를 이용한 DFS구현
|
1
2
3
4
5
6
7
8
9
10
|
bool visited3[7] = { false, };
void DFS2(Graph const& graph, int now) {
visited3[now] = true;
cout << now << ", ";//방문시 출력
for (auto v : graph.adList[now]) {//해당 노드가 갈 수 있는 곳 중에서
if(!visited3[v.first])//방문하지 않은 곳이면
DFS2(graph, v.first);//해당 destination 노드로 파고 들어가기
}
return;
}
|
cs |
1 : 방문을 확인하기 위한 공간
2 : 파라미터로 그래프와 현재 위치를 받아온다.
3 : 현재 위치에 방문 기록
5 : 현재 노드가 갈 수 있는 곳 중 방문하지 않은 곳을 다시 재귀호출한다. v.first에는 destination이 기록되어있다.
이후 재귀호출 된 위치가 방문으로 기록되고, 다시 위 과정을 반복한다.
9 : for문을 빠져나왔다면 더 이상 갈 곳이 없는 것이므로 종료 조건이 된다.
Breadth-First Search(BFS):너비 우선 탐색
Breadth-First Search (BFS) 너비 우선 탐색
BFS는 queue를 이용하여 구현될 수 있다. 동작은 현재 위치에서 이웃한 모든 노드를 동시에 방문한다. 그리고 방문한 노드는 재방문하지 않는다. 이 작업의 반복이다.
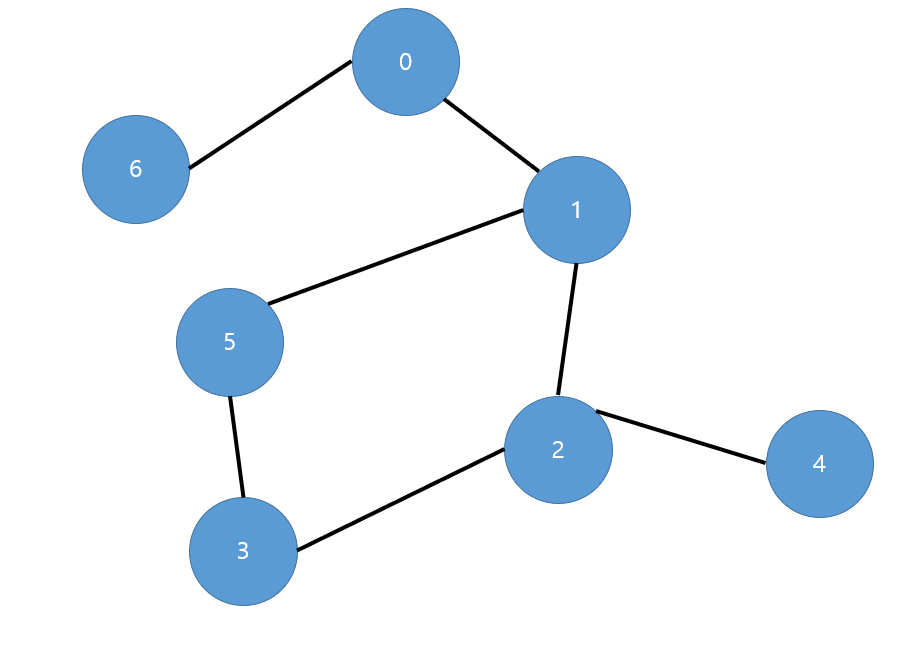
큐를 이용한 BFS구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
bool visited2[7] = { false, };
queue<int> q;
void BFS(Graph const& graph, int start) {
if (visited2[start] == false) {
visited2[start] = true;
q.push(start);
}
while (!q.empty()) {
int now = q.front();
for (auto v : graph.adList[now]) {
if (!visited2[v.first]) {//first = dest, second = weight
visited2[v.first] = true;
q.push(v.first);
}
}
cout << now << ", ";
q.pop();
}
}
|
cs |
4 : 시작 위치를 기록하고 큐에 넣는다.
8 : 큐가 비는 것이 종료 조건이다.
9 : 큐의 맨 앞을 현재 노드로 설정한다.
10 : 큐를 순회하며 갈 수 있는 곳들을 모두 큐에 넣고 방문처리한다.
17 : 현재 노드를 출력하고 pop한다.
이후 출력되는 것들은 현재 노드의 인근 모든 노드가 될 것이다. DFS에서는 끝까지 들어간 후 하나씩 출력하는 데에 반해 BFS는 퍼져나가며 출력한다는 것을 확인할 수 있다.
전체 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
|
#include <iostream>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
using namespace std;
struct Edge {
int src, dest, weight;
};
typedef pair<int, int> Pair;
class Graph {
public:
vector<vector<Pair>> adList;
Graph(vector<Edge> const& edges, int n) {
adList.resize(n);
for (auto& edge : edges) {
int src = edge.src;
int dest = edge.dest;
int weight = edge.weight;
adList[src].push_back(make_pair(dest, weight));
adList[dest].push_back(make_pair(src, weight));
sort(adList[src].begin(), adList[src].end());
}
}
};
void printGraph(Graph const& graph, int n) {
for (int i = 0; i < n; i++) {
for (Pair v : graph.adList[i]) {
cout << "(" << i << ", " << v.first << ", " << v.second << ") ";
}
cout << endl;
}
}
bool visited3[7] = { false, };
void DFS2(Graph const& graph, int now) {
visited3[now] = true;
for (auto v : graph.adList[now]) {//해당 노드가 갈 수 있는 곳 중에서
if(!visited3[v.first])//방문하지 않은 곳이면
DFS2(graph, v.first);//해당 destination 노드로 파고 들어가기
}
cout << now << ", ";//더 이상 파고 들어갈 곳이 없으면 출력
return;
}
bool visited[7] = { false, };
stack<int> s;
void DFS(Graph const& graph, int start) {
if (visited[start] == false) {
s.push(start);
visited[start] = true;
}
while (!s.empty()) {
int now = s.top();
for (auto v : graph.adList[now]) {
if (!visited[v.first]) {//first = dest, second = weight
visited[v.first] = true;
s.push(v.first);
}
}
if (s.top() == now) {//조건: for문을 통과했음에도 push된 요소가 없음, 즉 해당 노드가 말단이거나 visit가능한 노드가 존재하지 않음
s.pop();//더 이상 갈 곳이 없으면 pop하여 이전으로 돌아감
cout << now << ", ";
}
}
}
bool visited2[7] = { false, };
queue<int> q;
void BFS(Graph const& graph, int start) {
if (visited2[start] == false) {
visited2[start] = true;
q.push(start);
}
while (!q.empty()) {
int now = q.front();
for (auto v : graph.adList[now]) {
if (!visited2[v.first]) {//first = dest, second = weight
visited2[v.first] = true;
q.push(v.first);
}
}
cout << now << ", ";
q.pop();
}
}
int main() {
vector<Edge> edges = { {0, 6, 1}, {0, 1, 1}, {1, 2, 2}, {2, 3, 3}, {2, 4, 3}, {3, 5, 2}, {5, 1, 2} };
Graph graph = Graph(edges, 7);
printGraph(graph, 7);
cout << "DFS with stack" << endl;
DFS(graph, 0);
cout << endl;
cout << "DFS with recursion" << endl;
DFS2(graph, 0);
cout << endl;
cout << "BFS" << endl;
BFS(graph, 0);
return 0;
}
|
cs |

출력 결과:
(0, 1, 1) (0, 6, 1)
(1, 0, 1) (1, 2, 2) (1, 5, 2)
(2, 1, 2) (2, 3, 3) (2, 4, 3)
(3, 2, 3) (3, 5, 2)
(4, 2, 3)
(5, 1, 2) (5, 3, 2)
(6, 0, 1)
DFS with stack
0, 1, 2, 3, 5, 4, 6,
DFS with recursion
0, 1, 2, 3, 5, 4, 6,
BFS
0, 1, 6, 2, 5, 3, 4,
*각종 알고리즘 시뮬레이션 사이트
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
'컴퓨터 > 알고리즘:자료구조' 카테고리의 다른 글
| [알고리즘] 분할정복 알고리즘 정리/분할정복을 알아보자/(코드 및 시간복잡도) (1) | 2023.04.14 |
|---|---|
| [자료구조] C++트리 설명 및 구현(이진트리)/이진트리 구현 (0) | 2022.11.28 |
| [자료구조] C++ list자료구조 정리/list 함수/list예시 (0) | 2022.11.03 |
| [자료구조] C++ vector자료구조 정리/vector 함수 (0) | 2022.10.27 |
| [자료구조] c++ 배열(STL Array)의 각종 사용 방법/동적 할당, 함수 파라미터, 2차원 배열 (0) | 2022.10.02 |




댓글